(this utterly ridiculous suggestion from @taowplayer, I think he was drunk)
what makes a good bum
Aside from its obvious purpose, the main use of the human bottom is to make sitting down comfortable. In order to be comfortable, there’s a balance between the weight of the person in question and the amount of fat making up the buttocks, acting as a form of cushion. The simple answer to the question, then, is “fat enough to comfortably support the person when sitting down”.
Of course, what the person is sitting on also makes a difference. A foam-filled sofa cushion naturally supports you much more than a hard bicycle seat, and so a cyclist would perhaps benefit from more bottom fat than their weight would suggest. This is why most cyclists opt to wear padded cycling shorts and people who sit on beanbags wear bikinis.
Perhaps a more quantitative answer would be useful. In the UK, the average weight of a person is 76.9kg[ref]According to this BBC article, which is a little old now. I averaged the male and female weights.[/ref]. If we use this figure, we can calculate how much bottom fat is necessary to support the average human. Of course, we need to make some assumptions: the person is of average weight, they’re sat on a hard surface, all of their weight is transferred to their bottom (that is, they’re not leaning on anything or have their feet on the floor) and they have buttocks of equal size.
The Young’s Modulus of any material is the ratio of the stress on the object to the strain (the ratio of deformation over the initial length), and is in effect a measurement of the “squeezability” of the material. It is generally considered that pigs have a similar makeup to humans as far as adipose tissue (that’s fat to you and I) is concerned, and luckily for us experiments have been done[ref]Here, in fact.[/ref] on pig fat to determine a Young’s Modulus, which we can borrow for this purpose:
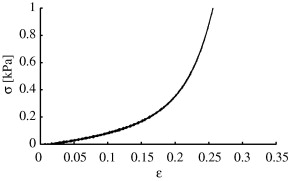
The Young’s Modulus, E, can be calculated using this formula:
![]()
Where F/A is the stress (force/area) and dL/L is strain (change in length/original length). We can see from the graph that when stress hits about 0.6kPa, the strain stops increasing much more – this is the point at which the fat is about as squashed as it’s going to get, and so can be suggested to be the point at which natural bumfat cushioning stops working. So we know that the maximum E is 0.6kPa (600Pa), F is 754.1N[ref]Force = Mass x Acceleration, so 76.9kg applies a force of 76.9 x 9.807 (standard gravity at is 9.807m/s2) = 754.1N[/ref], and strain is 0.25. In the formula:
![]()
Which can be rearranged to show that A = 5.03m2. Therefore, a posterior with a surface area of 5.03 square metres is ideal for the maximum amount of comfort. That’s quite large. In fact, it’s 2.24×2.24m in size.
Now let us assume that a bottom is roughly shaped like one quarter of a sphere. It isn’t, but that’s a close enough shape. To find the surface area of a sphere, we use this equation:
![]() which means that the surface area of a quarter sphere would be 1/4 of that, helpfully just Pi x r2. We know A is 5.03m2, and Pi is 3.14, so can rearrange to show that:
which means that the surface area of a quarter sphere would be 1/4 of that, helpfully just Pi x r2. We know A is 5.03m2, and Pi is 3.14, so can rearrange to show that:
![]()
Making r = 0.79m
Now, we can calculate the volume of the quarter sphere. The volume of a whole sphere is this:
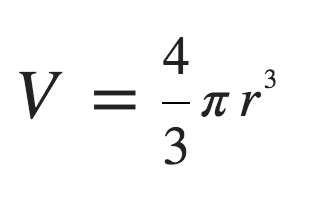
Which would be 2.07m3. So a quarter of that is about 0.52m3. Our final step is to use the density of adipose tissue (which is 0.9g/ml[ref]From here.[/ref], or 900kg/m3) to calculate the mass of fat needed to fill this sized bottom.
This is simply mass = volume x density, making mass = 0.52×900 = 468kg.
So the answer to the question “what makes a good bum”, is “have one that literally weighs about half a ton”. That, and the ability to balance a wine glass on it while still standing upright. Apparently.
Disclaimer: The maths and physics demonstrated here are mostly sound, but so many assumptions were made and actual figures were not properly checked, so the outcome was essentially nonsense.
(Featured image is from here, is unmodified, and used under this licence)

